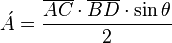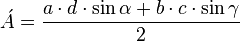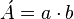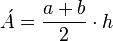características
Una propiedad de todos los triángulos es que la suma de las longitudes de dos de sus lados es siempre mayor que la longitud del tercer lado.
La suma de todos los ángulos de sus vértices, en un plano, es igual a 180°.
calculo de perímetro y área
Área y perímetro de un triángulo
Perímetro de un triángulo
El perímetro de un triángulo es igual a la suma de sus tres lados.
| Triángulo Equilátero | Triángulo Isósceles | Triángulo Escaleno |
 |  |  |
 |  |  |
Área de un triángulo
El área de un triángulo es igual a base por altura partido por 2.
La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).


Ejemplo
Hallar el área del siguiente triángulo:


Área de un triángulo equilátero



Ejemplo
Calcular el área de un triángulo equilátero de 10 cm de lado.
Área de un triángulo rectángulo
El área de un triángulo rectángulo es igual al producto de los catetos partido por 2.


Ejemplo
Calcular el área del triángulo rectángulo cuyos catetos miden 3 y 4 cm.


Semiperímetro
El semiperímetro de un triángulo es igual a la suma de sus lados partido por 2.
Se nombra con la letra p.
criterios de semejanza


Dados los triángulos ABC y A’B’C’, los lados a y a’, b y b’, c y c’ se llaman lados homólogos.
Los ángulos homólogos son:
Dos triángulos son semejantes cuando tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales.

La razón de la proporción entre los lados de los triángulos se llama razón de semejanza.
La razón de los perímetros de los triángulos semejantes es igual a su razón de semejanza.
La razón de las áreas de los triángulos semejantes es igual al cuadrado de su razón de semejanza.
teorema de pitágoras
El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.


Empleo del teorema de Pitágoras
Conociendo los lados de un triángulo, averiguar si es rectángulo
Para que un triángulo sea rectángulo el cuadrado de lado mayor ha de ser igual a la suma de los cuadrados de los dos menores.
Determinar si el triángulo es rectángulo.


Conociendo los dos catetos calcular la hipotenusa
Los catetos de un triángulo rectángulo miden en 3 m y 4 m respectivamente. ¿Cuánto mide lahipotenusa?


Conociendo la hipotenusa y un cateto, calcular el otro cateto
La hipotenusa de un triángulo rectángulo mide 5 m y uno de sus catetos 3 m. ¿Cuánto mide otro cateto?


c)cuadriláteros
características
- La suma de sus ángulos internos siempre da como resultado 360º.
Por lógica todos los cuadriláteros son cuadrángulos, ya que esta definición se aplica a lospolígonos de cuatro ángulos.
- La suma de sus ángulos internos siempre da como resultado 360º.
Por lógica todos los cuadriláteros son cuadrángulos, ya que esta definición se aplica a lospolígonos de cuatro ángulos.
clasificación
Los cuadriláteros se clasifican en:
Paralelogramos: sus lados opuestos son paralelos Rectángulos Cuadrado Rectángulo Oblicuángulos Rombo Romboide Trapecios: dos lados paralelos; los otros dos, no Trapecio rectángulo Trapecio isósceles Trapecio escaleno Trapezoide: lados no paralelos Trapezoide simétrico o deltoide Trapezoide asimétricocálculo del perímetro y área
El perímetro de un cuadrilátero es la longitud de la línea cerrada que lo bordea, es decir, la suma de las longitudes de sus cuatro lados. | |
Calcula y escribe en tu cuaderno el valor del perímetro de los cuadriláteros que has construido en los ejercicios de la página anterior. | |
En la escena adjunta mueve los vertices B, C y D del cuadrilátero para construir esos cuadriláteros y en cada caso comprueba el resultado del perímetro que has hallado con el que aparece en la figura. |
Área de un cuadrilátero
- El área también se puede obtener mediante triangulación:
- Siendo:
 el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
. el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
.
- El rectángulo es un paralelogramo cuyos ángulos son todos de 90º, y el área es igual al producto de dos de sus lados contiguos a y b:4
- El rombo es un paralelogramo, cuyos 4 lados son iguales, y tiene su área dada por el semiproducto de sus dos diagonales:
- El cuadrado es el polígono regular de cuatro lados; es a la vez un rectángulo y un rombo, por lo que su área puede ser calculada de la misma manera que la de estos dos. En particular, dado que sus lados son iguales, se usa la fórmula:4
- El trapecio, el cual tiene dos lados opuestos paralelos entre sí y dos lados no paralelos, tiene un área que viene dada por la media aritmética de sus lados paralelos multiplicado por la distancia entre ellos (altura):4
d) círculo
angulos
Ángulo central: cuando un ángulo tiene su vértice en el centro del círculo.
Ángulo inscrito: los extremos y el vértice están sobre la circunferencia.
Ángulo semi-inscrito: formado por una cuerda y una recta tangente.
En un círculo de radio uno, la amplitud de un ángulo central coincide con la longitud del arco que subtiende, así, un ángulo central recto mide π/2 radianes, y la longitud del arco es π/2; si el radio mide r, el arco medirá r x π/2.
La longitud de un arco de ángulo central α, dado en grados sexagesimales, medirá 2π x r x α / 360.
Un ángulo inscrito mide la mitad del arco que subtiende, sin importar la posición del vértice. Un ángulo semi-inscrito mide la mitad del arco que se encuentra entre la cuerda y la tangente
calculo del perímetro y área
Perímetro del Círculo
El perímetro de un círculo es una circunferencia y su ecuación es:
 (en función del radio).
(en función del radio).
o
 (en función del diámetro).
(en función del diámetro).
donde  es el perímetro,
es el perímetro,  es la constante matemática pi (
es la constante matemática pi ( ),
), es el radio y
es el radio y  es el diámetro del círculo.
es el diámetro del círculo.
Área del círculo
Existen numerosas fórmulas para calcular el área de un círculo. Un círculo de radio  , tendrá un área:
, tendrá un área:
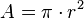 ; en función del radio (r).
; en función del radio (r).
o
 ; en función del diámetro (d), pues
; en función del diámetro (d), pues 
o
 ; en función de la longitud de la circunferencia máxima (C),
; en función de la longitud de la circunferencia máxima (C),
pues la longitud de dicha circunferencia es: 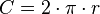
elementos

Centro: Es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.
Radio:Punto del que equidistan todos los puntos de la circunferencia.
Segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Elementos de la circunferencia
Cuerda

Segmento que une dos puntos de la circunferencia.
Diámetro

Cuerda que pasa por el centro.
Arco

Cada una de las partes en que una cuerda divide a la circunferencia. Se suele asociar a cada cuerda el menor arco que delimita.
Semicircunferencia

Cada uno de los arcos iguales que abarca un diámetro.
Círculo

Es la figura plana comprendida en el interior de una circunferencia.
Elementos de un círculo
Segmento circular

Porción de círculo limitada por una cuerda y el arco correspondiente.
Semicírculo

Porción del círculo limitada por un diámetro y el arco correspondiente. Equivale a la mitad del círculo.
Zona circular

Porción de círculo limitada por dos cuerdas.
Sector circular

Porción de círculo limitada por dos radios.
Corona circular

Porción de círculo limitada por dos círculos concéntricos.
Trapecio circular

Porción de círculo limitada por dos radios y una corona circular.