Efecto Fotoeléctrico
Ocurre cuando la luz (visible o ultravioleta) incide sobre determinadas superficies metálicas y estas emiten electrones (fotoelectrones).
Medidas del Efecto Fotoeléctrico
- Los electrones emitidos al iluminar el cátodo originan una corriente eléctrica de intensidad al chocar con el ánodo. La intensidad medida es proporcional al número de electrones arrancados.
- El trabajo (W) necesario para arrancar el electrón del metal depende de su energía de enlace con este. La energía más pequeña, correspondiente a los electrones más débilmente unidos, recibe el nombre de función trabajo del metal o trabajo de extracción.
- Ánodo positivo → atraerá a los electrones.
- Ánodo negativo → los electrones serán repelidos y solo llegarán a él aquellos que tengan una energía cinética inicial suficiente para vencer el potencial de repulsión.
Hechos Inexplicables por la Física Clásica
- La emisión tiene lugar sólo si la frecuencia (f) de la radiación supera una frecuencia mínima, propia de cada metal, llamada frecuencia umbral (fu). Según la teoría clásica, el efecto fotoeléctrico debería ocurrir para cualquier frecuencia de la luz siempre que esta fuese lo suficientemente intensa.
- Si la frecuencia (f) de la luz incidente es mayor que la frecuencia umbral (fu) (f > fu), el número de electrones emitidos es proporcional a la intensidad de la radiación incidente. Sin embargo, su energía cinética máxima es independiente de la intensidad de la luz, lo cual no tiene explicación en la teoría clásica.
- Nunca se ha podido medir un tiempo de retraso entre la iluminación del metal y la emisión de los fotoelectrones. Sin embargo, según la teoría clásica, si la intensidad de luz es muy débil, debe existir un tiempo de retraso entre el instante en que la luz incide sobre la superficie metálica y la emisión de fotoelectrones.
La teoría cuántica de Einstein puso en duda la teoría clásica de la luz. Propuso una nueva teoría y utilizó el efecto fotoeléctrico para probar cuál de las dos teorías era la correcta.
Según la hipótesis de Planck, únicamente está cuantizada la energía al ser emitida o absorbida por los osciladores. En cambio, según Einstein, toda la energía emitida por una fuente radiante está cuantizada en paquetes que se denominan fotones.
El trabajo (W) necesario para arrancar el electrón del metal depende de su energía de enlace con este. La energía más pequeña, correspondiente a los electrones más débilmente unidos, recibe el nombre de trabajo de extracción W0= h·fu
Ley de Faraday y Lenz para la Inducción Electromagnética
Valor de la Fuerza Electromotriz Inducida. Sentido de la Corriente.
La inducción electromagnética es la aparición de una corriente eléctrica cuando varía el número de líneas de inducción magnética en un circuito.
- Si se acerca o aleja un imán a una espira, en esta se genera una corriente eléctrica inducida. Ocurre durante el movimiento del imán. Si la bobina se invierte, cambia el sentido. La corriente inducida cesa cuando finaliza el movimiento relativo espira-imán.
- → La intensidad de corriente inducida depende de la velocidad y de la intensidad del campo magnético del imán, además del número de espiras de la bobina.
- Cuando se abre o cierra un circuito también se detectan corrientes inducidas. Se induce corriente en la 2ª bobina mientras que aumenta o disminuye la intensidad de corriente de la 1ª bobina
→ La inducción eléctrica es debida a campos magnéticos variables.
Flujo Magnético
El flujo de un campo magnético (Φ) es una medida de la cantidad de líneas de campo que atraviesan una superficie.
Φ = NBScosθ
- Φ = Flujo (Wb)
- B = Intensidad del campo magnético (T)
- S = Superficie (m2) → El vector superficie es perpendicular a la superficie que representa.
- θ = Ángulo formado entre los vectores del campo y la superficie.
- N = Número de espiras.
Ley de Lenz 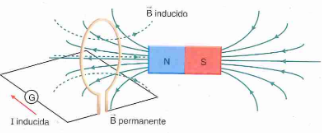
El sentido de la corriente inducida es tal que se opone a la causa que la produce. Podemos inducir una corriente en un circuito variando cada uno de los 3 factores que intervienen en la siguiente expresión: Φ = BScosθ
Ley de Faraday
La fuerza electromotriz inducida (fem) en un circuito es igual a la velocidad con la que varía el flujo magnético a través de dicho circuito.
Con la resistencia eléctrica y con la fem podemos calcular la intensidad aplicando la ley de Ohm: I = fem / R = -1
Campos Magnéticos Producidos por Corrientes. Ley de Biot-Savart
En 1820 H.C. Oersted descubrió que una corriente eléctrica desviaba la aguja imantada de una brújula. Esta experiencia puso de manifiesto que electricidad y magnetismo están estrechamente relacionados.
Corriente Rectilínea Indefinida
Una corriente rectilínea indefinida crea un campo magnético en un punto situado a una distancia del hilo conductor.
Dividimos el hilo en pequeños elementos de corriente Idl. Según la ley de Biot y Savart, la contribución de un elemento de corriente es:
La contribución al campo de cada elemento de corriente tiene la misma dirección, tangente a una circunferencia centrada en el hilo conductor. El campo total se podrá calcular sumando los módulos de todas las contribuciones. El elemento de longitud dl coincide con dz (dl=dz) y se relaciona con el ángulo θ. Sustituimos estas expresiones en el campo magnético y sumamos todas las contribuciones: B = …
La dirección de B es perpendicular al hilo conductor y al segmento a, y su sentido viene determinado por la regla de la mano derecha.
Corriente Circular
Dividimos la espira en pequeños elementos de corriente I dl. Según la ley de Biot y Savart, la contribución de un elemento de corriente es:
dB = …
(B, l y u → vectores)
La contribución de cada elemento de corriente al campo magnético tiene la misma dirección y sentido. Por tanto, el campo magnético total se podrá calcular sumando los módulos de todas las contribuciones:
B = …
Donde hemos tenido en cuenta que la integral de dl a lo largo de toda la espira es su longitud: 2πR
La dirección de B es perpendicular al plano de la espira y su sentido viene determinado por la regla de la mano derecha.
Fuerzas Entre Corrientes Eléctricas. Caso de Dos Hilos Rectos, Paralelos e Infinitos.
Si tenemos un hilo conductor rectilíneo por donde circula una corriente eléctrica y que atraviesa un campo magnético, se origina una fuerza electromagnética sobre el hilo. Esto es debido a que el campo magnético genera fuerzas sobre cargas eléctricas en movimiento.
Si las corrientes eléctricas tenían el mismo sentido, los hilos se atraían; mientras que si las corrientes eran de sentidos contrarios, los hilos se repelían.
Supondremos que la longitud (l) de los conductores es mucho mayor que su separación (d), de modo que podamos aplicar los resultados obtenidos para corrientes indefinidas. Entonces, el campo magnético que el conductor 1 crea a una distancia d es: B = …
El vector B es perpendicular al conductor 2. Por tanto, la fuerza que ejerce el conductor 1 sobre el conductor 2 es:
F = …
La fuerza ejercida por el conductor 2 sobre el conductor 1, F21, tiene el mismo módulo y dirección, pero sentido contrario, pues estas fuerzas cumplen el principio de acción y reacción: F21 = -F12
La fuerza que experimentan los conductores por unidad de longitud es:
F = …
Definición de Amperio
Es la intensidad de corriente eléctrica que circula por dos conductores rectilíneos paralelos e indefinidos, separados una distancia de un metro en el vacío, cuando ambos se atraen o se repelen con una fuerza de 2·10-7 N por metro de longitud.
Fuerza Ejercida Dentro de un Campo Magnético Uniforme
Al estudiar el concepto de inducción magnética habíamos indicado que la fuerza ejercida por un campo magnético sobre una carga eléctrica verifica las siguientes propiedades:
- Si la carga está en reposo, no actúa ninguna fuerza sobre ella.
- Si la carga se mueve con una velocidad (v), experimenta una fuerza magnética con las siguientes características:
- Es proporcional al valor de la carga (q).
- Es perpendicular a la velocidad (v).
- Su módulo depende de la dirección de la velocidad: si el vector v tiene una cierta dirección, la fuerza magnética es nula; si el vector v es perpendicular a la dirección anterior, la fuerza magnética es máxima.
Ley de Lorentz
Estas propiedades pueden ser resumidas en una ecuación vectorial que recibe el nombre de Ley de Lorentz: F = q(v x B)
Si una carga positiva entra en un campo magnético uniforme, la fuerza de Lorentz le obligará a seguir un movimiento circular uniforme. Podemos relacionar el radio (R) de la circunferencia con la inducción magnética (B) y la velocidad (v) de la carga.
La fuerza centrípeta que actúa sobre la carga es justamente la fuerza de Lorentz, F = qvB.
F = ma = m(v2/R) ⇒ qvB = m(v2/R)
De donde obtenemos el radio de la circunferencia descrita por q. R = (mv) / (qB)
Fuerza Magnética Sobre un Elemento de Corriente
Un conductor por el que circula una corriente eléctrica, experimenta una fuerza (F) cuando se sitúa dentro de un campo magnético. Esa F es la resultante de las fuerzas de Lorentz que el campo ejerce sobre las cargas que forman esa corriente.
DIBUJO
- I dl = Elemento de corriente
- dt = Tiempo en el que la carga eléctrica transporta el movimiento dt es dq = Idt
- v = Velocidad
Si todas las cargas tienen la misma velocidad → La fuerza de Lorentz en una corriente se puede escribir así:
dF = dq(v x B) = Idt(v x B) = (vdt x B) (la x es multiplicación)
Como vdt es el vector dl, la ecuación se quedaría así: dF = I(dl x B)
Para determinar Fm que actúa en un conductor (c):
- → Descomponer en elementos de corriente
- → Sumar fuerzas
En el caso de un hilo conductor:
F = I(l x B) → Módulo F = I l B senθ
Explicación:
- l = Longitud
- B = Campo magnético uniforme
- I = Vector de módulo/ con dirección y sentido de la intensidad de la corriente
- θ = Ángulo que forman los vectores l y B
Si todas las cargas tienen la misma velocidad → La fuerza de Lorentz en una corriente se puede escribir así: dF = dq(v x B) = Idt(v x B) = (vdt x B) (la x es multiplicación) Como vdt es el vector dl, la ecuación se quedaría así: dF = I(dl x B) Para determinar Fm que actúa en un conductor (c) → Descomponer en elementos de corriente
→ Sumar fuerzas
En el caso de un hilo conductor:
F = I(l x B) → Módulo F = I l B senθ
Explicación:
- l = Longitud
- B = Campo magnético uniforme
- I = Vector de módulo/ con dirección y sentido de la intensidad de la corriente
- θ = Ángulo que forman los vectores l y B
